V
voska89
Moderator
- Joined
- Jul 7, 2023
- Messages
- 42,387
- Reaction score
- 0
- Points
- 36
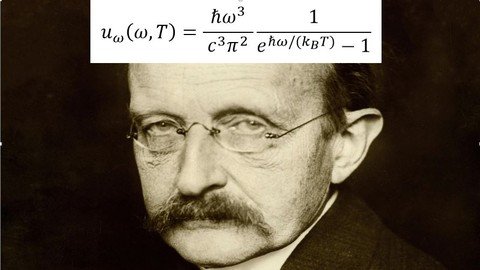
Free Download Statistical Physics - Relation To Quanta And Thermodynamics
Last updated 11/2023
MP4 | Video: h264, 1280x720 | Audio: AAC, 44.1 KHz
Language: English | Size: 6.87 GB | Duration: 7h 51m
The mathematics used in the discovery of quantum physics, the foundations of thermodynamics, phase transitions.
What you'll learn
Planck's mathematical trick which led to the discovery of quantum physics
rigorous definition of entropy
history of the physics of the 1900's
Basics of Statistical Mechanics
Einstein's papers on thermodynamics
Brownian motion
Lioville theorem
Ideal gas law
photoelectric effect
canonical transformations
Hamilton equations
Black body problem
Phase transitions
Requirements
Calculus (especially derivatives, integrals, limits)
Multivariable Calculus
Basics of Fourier Analysis
For the second part of the course: Lagrange equations, phase space variables (position and momentum)
Description
First part of the course:The first part of the course showcases the beautiful mathematics that, in the late 19th century/ early 20th century, led to the discovery of a revolutionary branch in physics: Quantum Mechanics. Planck postulated that the energy of oscillators in a black body is quantized. This postulate was introduced by Max Planck in his derivation of his law of black body radiation in 1900. This assumption allowed Planck to derive a formula for the entire spectrum of the radiation emitted by a black body (we will also derive this spectrum in this course). Planck was unable to justify this assumption based on classical physics; he considered quantization as being purely a mathematical trick, rather than (as is now known) a fundamental change in the understanding of the world. In 1905, Albert Einstein adapted the Planck postulate to explain the photoelectric effect, but Einstein proposed that the energy of photons themselves was quantized (with photon energy given by the Planck-Einstein relation), and that quantization was not merely a "mathematical trick". Planck's postulate was further applied to understanding the Compton effect, and was applied by Niels Bohr to explain the emission spectrum of the hydrogen atom and derive the correct value of the Rydberg constant.In addition to the very useful mathematical tools that will be presented and discussed thoroughly, the students have the opportunity to learn about the historical aspects of how Planck tackled the blackbody problem.Calculus and multivariable Calculus are a prerequisite to the course; other important mathematical tools (such as: Fourier Series, Perseval's theorem, binomial coefficients, etc.) will be recalled, with emphasis being put on mathematical and physical insights rather than abstract rigor.Second part of the courseBy the end of June 1902, just after being accepted as Technical Assistant at the Federal Patent Office in Bern, Albert Einstein, 23, sent to the renowned journal Annalen der Physik a manuscript with the bold title "Kinetic Theory of Thermal Equilibrium and of the Second Law of Thermodynamics". In the introduction, he explains that he wishes to fill a gap in the foundations of the general theory of heat, "for one has not yet succeeded in deriving the laws of thermal equilibrium and the second law of thermodynamics using only the equations of mechanics and the probability calculus". He also announces "an extension of the second law that is of importance for the application of thermodynamics". Finally, he will provide "the mathematical expression of the entropy from the standpoint of mechanics". In particular, in the second part of the course we will see the mathematics Einstein used in his paper from 1902.Besides, other concepts from Classical mechanics are explained, such as Liouville's theorem (this theorem is used by Einstein in his article), as well as Hamilton equations and more.For the second part, the student should already be familiar with phase space and other concepts from classical physics (such as Lagrange equations).Third part of the courseIn the third part of the course some of the articles of Einstein's Annus Mirabilis are explained. In particular, the article on the photoelectric effect and that on the Brownian motion.Fourth part of the courseIn the last section of this course we focus on the derivation of phase transitons from the Ising model. All the previous sections will be useful in contextualizing this last part of the course.
Overview
Section 1: Introduction
Lecture 1 Introduction
Lecture 2 Introduction to the blackbody problem
Lecture 3 Definition of blackbody
Section 2: Analysis of blackbody cavities
Lecture 4 Irrelevance of Shape of the Cavity
Lecture 5 Wave equation for Electromagnetic Waves
Lecture 6 Solution to the Wave Equation
Lecture 7 Compliance with Boundary Conditions
Lecture 8 Number of Modes per Frequency
Lecture 9 Average Energy per Mode
Section 3: Quantization: Systems of Particles
Lecture 10 Distribution of the Average Energy, Planck's idea
Lecture 11 Systems of Particles, Binomial Coefficient
Lecture 12 Number of Arrangements of the Particles into the Energy Levels
Lecture 13 Sterling's Approximation
Lecture 14 Getting ready to maximize the Number of Arrangements
Section 4: Derivation of the Average Energy per Mode
Lecture 15 Maximizing the Number of Arrangements
Lecture 16 Expression for the Energy per Mode
Lecture 17 Planck's Mathematical Trick
Lecture 18 Calculation of the Average Energy per Mode part 1
Lecture 19 Calculation of the Average Energy per Mode part 2
Section 5: Derivation of the Stefan-Boltzman Law
Lecture 20 Classical vs Quantum
Lecture 21 Energy per Volume per Wavelength and Energy per Volume
Lecture 22 Planck's Integral
Lecture 23 Brief Summary of Fourier Analysis
Lecture 24 Parseval's Theorem
Lecture 25 Ultraviolet Catastrophe and Energy per Unit Surface
Lecture 26 Calculation of the Series 1/n^4
Lecture 27 Putting Results Together
Lecture 28 Deriving the Stefan-Boltzmann Law part1
Lecture 29 Deriving the Stefan-Boltzmann Law part2
Section 6: Useful appendix to the first part of the course
Lecture 30 Derivation of the Maxwell Boltzmann distribution
Lecture 31 Planck's idea for the mathematical solution to the black body problem
Lecture 32 How Planck derived the black-body radiation law the first time
Section 7: Einstein's article on thermodynamics from 1902
Lecture 33 The mathematics that Einstein used in one of his papers on thermodynamics part 1
Lecture 34 The mathematics that Einstein used in one of his papers on thermodynamics part 2
Lecture 35 The mathematics that Einstein used in one of his papers on thermodynamics part 3
Lecture 36 The mathematics that Einstein used in one of his papers on thermodynamics part 4
Lecture 37 The mathematics that Einstein used in one of his papers on thermodynamics part 5
Lecture 38 Mathematical proof of Liouville's theorem
Lecture 39 Canonical transformations and generating functions
Lecture 40 Hamilton equations derived from a variational principle
Lecture 41 Variation principle derived from Newton's second law
Lecture 42 Simple proof of Liouville's theorem
Lecture 43 Einstein's different approach for the derivation of the entropy
Lecture 44 Ideal gas law derived from Statistical Mechanics
Section 8: Einstein's article on the photoelectric effect, which ushered in Quantum Physics
Lecture 45 Part 1 of Einstein's article on the photoelectric effect
Lecture 46 Part 2 of Einstein's article on the photoelectric effect
Lecture 47 Part 3 of Einstein's article on the photoelectric effect
Lecture 48 Part 4 of Einstein's article on the photoelectric effect
Section 9: Einstein article on Brownian motion
Lecture 49 step-by-step explanation of Einstein's article on the Brownian motion
Section 10: Entropy derivation from Classical Mechanics
Lecture 50 part 1: Entropy as a Function of State and How to Derive it from Lagrange Eqs
Lecture 51 part 2: Entropy as a Function of State and How to Derive it from Lagrange Eqs
Lecture 52 part 3: Entropy as a Function of State and How to Derive it from Lagrange Eqs
Section 11: Phase transitions and the Ising model
Lecture 53 Ising model and effective free energy
Lecture 54 Mean field Theory in the Ising model
Lecture 55 Landau approach to phase transitions
Lecture 56 Discontinuity in the heat capacity
physics students,mathematics students,anyone interested in the historical fascinating origin of Quantum Physics,anyone interested in the mathematics used by Einstein in 1902 dealing with thermodynamics,anyone who seeks an in-depth understanding of entropy,Students who would like to improve their reasoning and insights in solving physical problems,anyone interested in explanations given through the lens of mathematics,engineering students
Homepage
Code:
https://www.udemy.com/course/the-mathematical-beauty-that-led-to-quantum-physics/Recommend Download Link Hight Speed | Please Say Thanks Keep Topic Live
Rapidgator
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part4.rar.html
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part1.rar.html
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part6.rar.html
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part5.rar.html
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part3.rar.html
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part2.rar.html
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part8.rar.html
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part7.rar.html
Uploadgig
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part2.rar
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part8.rar
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part1.rar
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part5.rar
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part6.rar
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part7.rar
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part3.rar
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part4.rar
NitroFlare
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part3.rar
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part6.rar
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part7.rar
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part1.rar
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part4.rar
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part5.rar
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part2.rar
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part8.rar
Fikper
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part3.rar.html
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part2.rar.html
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part6.rar.html
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part8.rar.html
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part5.rar.html
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part4.rar.html
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part1.rar.html
rvptm.Statistical.Physics.Relation.To.Quanta.And.Thermodynamics.part7.rar.html
No Password - Links are Interchangeable
